LeetCode刷题目录2

发表于
字数统计: 9,555 | 阅读时长 ≈ 40分钟

树

递归

1. 树的高度

2. （判断是否）平衡树

3. 两节点的最长路径

4. 翻转树

1
2
3
4
5
6
7
8
9
10
11
12
输入：
	 4
   /   \
  2     7
 / \   / \
1   3 6   9
输出：
     4
   /   \
  7     2
 / \   / \
9   6 3   1

5. 归并两棵树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
Input:
       Tree 1                     Tree 2
          1                         2
         / \                       / \
        3   2                     1   3
       /                           \   \
      5                             4   7
Output:
         3
        / \
       4   5
      / \   \
     5   4   7

6. 判断路径和是否等于一个数

1
2
3
4
5
6
7
8
9
10
11
Given the below binary tree and sum = 22,
              5
             / \
            4   8
           /   / \
          11  13  4
         /  \      \
        7    2      1
return true, as there exist a root-to-leaf path 5->4->11->2 which sum is 22.

7. 统计路径和等于一个数的路径数量

路径不一定以 root 开头，也不一定以 leaf 结尾，但是必须连续。

思路：在函数里定义一个withRoot的函数，在withRoot函数体里也进行递归调用

8. 子树

思路：在函数里定义一个withRoot的函数，在withRoot函数体里也进行递归调用

9. 树的对称

1
2
3
4
5
6
7
8
9
10
11
   	1								
   / \
  2   2
 / \ / \
3  4 4  3  是对称。
 
 	1
   / \
  2   2
   \   \
   3    3不是对称

有点像8

10. 最小路径

树的根节点到叶子节点的最小路径长度

思路：注意和求树的高度不同

1
2
3
4
5
6
7
public int minDepth(TreeNode root) {
    if (root == null) return 0;
    int left = minDepth(root.left);
    int right = minDepth(root.right);
    if (left == 0 || right == 0) return left + right + 1;
    return Math.min(left, right) + 1;
}

11. 统计左叶子节点的和

1
2
3
4
5
6
7
  	3
   / \
  9  20
    /  \
   15   7
There are two left leaves in the binary tree, with values 9 and 15 respectively. Return 24.

12. 相同节点值的最大路径长度

给定一个二叉树，找到最长的路径，这个路径中的每个节点具有相同值。 这条路径可以经过也可以不经过根节点。

注意：两个节点之间的路径长度由它们之间的边数表示。

    5
   / \
  4   5
 / \   \
1   1   5   输出2

​
​ 1
​ / \
​ 4 5
​ / \ \
​ 4 4 5 输出2

不好想。。

13. 间隔遍历

如果两个直接相连的房子在同一天晚上被打劫，房屋将自动报警。计算在不触动警报的情况下，小偷一晚能够盗取的最高金额。

1
2
3
4
5
6
	 3
    / \
   2   3
    \   \
     3   1
Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.

14. 找出二叉树中第二小的节点

给定一个非空特殊的二叉树，每个节点都是正数，并且每个节点的子节点数量只能为 2 或 0。如果一个节点有两个子节点的话，那么这个节点的值不大于它的子节点的值。

给出这样的一个二叉树，你需要输出所有节点中的第二小的值。如果第二小的值不存在的话，输出 -1 。

1
2
3
4
5
6
7
8
Input:
   2
  / \
 2   5
    / \
    5  7
Output: 5

层次遍历

1. 一棵树每层节点的平均数

2. 得到左下角的节点

1
2
3
4
5
6
7
8
9
10
11
12
Input:
        1
       / \
      2   3
     /   / \
    4   5   6
       /
      7
Output:
7

思路：层次遍历进队时先进右节点。

前中后序遍历

1. 非递归实现二叉树的前序遍历

写法有点像层次遍历的写法，只不过用的是栈

2. 非递归实现二叉树的后序遍历

在非递归前序遍历基础上改造：

前序遍历为 root -> left -> right，后序遍历为 left -> right -> root。可以修改前序遍历成为 root -> right -> left，那么这个顺序就和后序遍历正好相反。

3. 非递归实现二叉树的中序遍历

思路：定义一个要伸到最左边的指针和一个栈，2层while循环。步骤：先伸到最左边，然后出栈入栈。

二叉查找树（BST）

1. 修剪二叉查找树

给定一个二叉搜索树，同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树，使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点，所以结果应当返回修剪好的二叉搜索树的新的根节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Input:
    3
   / \
  0   4
   \
    2
   /
  1
  L = 1
  R = 3
Output:
      3
     /
   2
  /
 1

思路：递归

2. 寻找二叉查找树的第 k 个元素

思路:1中序遍历（不使用额外空间，中序递归遍历的过程中就去找k）2递归解法（）

3. 把二叉查找树每个节点的值都加上比它大的节点的值

给定一个二叉搜索树（Binary Search Tree），把它转换成为累加树（Greater Tree)，使得每个节点的值是原来的节点值加上所有大于它的节点值之和。

例如：

输入: 二叉搜索树:
5
/ \
2 13

输出: 转换为累加树:
18
/ \
20 13

思路：递归。先遍历右子树。

4. 二叉查找树的最近公共祖先（LCA）

1
2
3
4
5
6
7
8
9
        _______6______
      /                \
  ___2__             ___8__
 /      \           /      \
0        4         7        9
        /  \
       3   5
For example, the lowest common ancestor (LCA) of nodes 2 and 8 is 6. Another example is LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
1
2
3
4
5
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    if (root.val > p.val && root.val > q.val) return lowestCommonAncestor(root.left, p, q);
    if (root.val < p.val && root.val < q.val) return lowestCommonAncestor(root.right, p, q);
    return root;
}

5. 二叉树的最近公共祖先(LCA)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
		____3______
      /              \
  ___5__           ___1__
 /      \         /      \
6        2       0        8
        /  \
       7    4
For example, the lowest common ancestor (LCA) of nodes 5 and 1 is 3. Another example is LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    if (root == null || root == p || root == q) return root;
    TreeNode left = lowestCommonAncestor(root.left, p, q);
    TreeNode right = lowestCommonAncestor(root.right, p, q);
    return left == null ? right : right == null ? left : root;
}

6. 从有序数组中构造二叉查找树

思路：递归，构造过程类似二分查找。数组索引中点即为根节点。

7. 根据有序链表构造平衡的二叉查找树

思路：递归，同上。找链表的中点需要定义一组快慢指针。

8. 在二叉查找树中寻找两个节点，使它们的和为一个给定值

653. Two Sum IV - Input is a BST (Easy)

1
2
3
4
5
6
7
8
9
10
11
Input:
    5
   / \
  3   6
 / \   \
2   4   7
Target = 9
Output: True

使用中序遍历得到有序数组之后，再利用双指针对数组进行查找。

9. 在二叉查找树中查找两个节点之差的最小绝对值

1
2
3
4
5
6
7
8
9
10
11
Input:
   1
    \
     3
    /
   2
Output:
1

利用二叉查找树的中序遍历为有序的性质，计算中序遍历中临近的两个节点之差的绝对值，取最小值。(在中序遍历递归过程中就进行最小值的比较)

10. 寻找二叉查找树中出现次数最多的值

给定一个有相同值的二叉搜索树（BST），找出 BST 中的所有众数（出现频率最高的元素）。

假定 BST 有如下定义：

结点左子树中所含结点的值小于等于当前结点的值
结点右子树中所含结点的值大于等于当前结点的值
左子树和右子树都是二叉搜索树

提示：如果众数超过1个，不需考虑输出顺序

进阶：你可以不使用额外的空间吗？（假设由递归产生的隐式调用栈的开销不被计算在内）

1
2
3
4
5
6
7
 1
    \
     2
    /
   2
return [2].

思路：中序遍历

trie todo

1树的高度2平衡树3两节点的最长路径 在递归过程中都要算树的高度1 + Math.max(l, r);注意带根节点和不带根节点（6,7,8）；注意递归函数的参数是左右节点即2个参数时的递归出口条件if (t1 == null && t2 == null) return true;if (t1 == null || t2 == null) return false; (8,9)

层次遍历写法；前中后序遍历非递归写法。

中序遍历在BST中的应用（2,8,9,10）；有序数组（链表）构造平衡二叉搜索树（6,7）；LCA(4,5)

分治

1. 给表达式加括号

给定一个含有数字和运算符的字符串，为表达式添加括号，改变其运算优先级以求出不同的结果。你需要给出所有可能的组合的结果。有效的运算符号包含 +, - 以及 * 。

示例 1:

输入: “2-1-1”
输出: [0, 2]
解释:
((2-1)-1) = 0
(2-(1-1)) = 2

思路：分治，递归。遍历运算符，以运算符左右2边的可能性做组合。

2. 不同的二叉搜索树

给定一个数字 n，要求生成所有值为 1…n 的二叉搜索树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Input: 3
Output:
[
  [1,null,3,2],
  [3,2,null,1],
  [3,1,null,null,2],
  [2,1,3],
  [1,null,2,null,3]
]
Explanation:
The above output corresponds to the 5 unique BST's shown below:
   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

解法二 递归
解法一完全没有用到查找二叉树的性质，暴力尝试了所有可能从而造成了重复。我们可以利用一下查找二叉树的性质。左子树的所有值小于根节点，右子树的所有值大于根节点。

所以如果求 1…n 的所有可能。

我们只需要把 1 作为根节点，[ ] 空作为左子树，[ 2 … n ] 的所有可能作为右子树。

2 作为根节点，[ 1 ] 作为左子树，[ 3…n ] 的所有可能作为右子树。

3 作为根节点，[ 1 2 ] 的所有可能作为左子树，[ 4 … n ] 的所有可能作为右子树，然后左子树和右子树两两组合。

4 作为根节点，[ 1 2 3 ] 的所有可能作为左子树，[ 5 … n ] 的所有可能作为右子树，然后左子树和右子树两两组合。

…

n 作为根节点，[ 1… n ] 的所有可能作为左子树，[ ] 作为右子树。

至于，[ 2 … n ] 的所有可能以及 [ 4 … n ] 以及其他情况的所有可能，可以利用上边的方法，把每个数字作为根节点，然后把所有可能的左子树和右子树组合起来即可。

如果只有一个数字，那么所有可能就是一种情况，把该数字作为一棵树。而如果是 [ ]，那就返回 null。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
public List<TreeNode> generateTrees(int n) {//抄的
        List<TreeNode> ans = new ArrayList<TreeNode>();
        if (n == 0) {
            return ans;
        }
        return getAns(1, n);
    }
    private List<TreeNode> getAns(int start, int end) {
        List<TreeNode> ans = new ArrayList<TreeNode>();
        //此时没有数字，将 null 加入结果中
        if (start > end) {
            ans.add(null);
            return ans;
        }
        //只有一个数字，当前数字作为一棵树加入结果中
        if (start == end) {
            TreeNode tree = new TreeNode(start);
            ans.add(tree);
            return ans;
        }
        //尝试每个数字作为根节点
        for (int i = start; i <= end; i++) {
            //得到所有可能的左子树
            List<TreeNode> leftTrees = getAns(start, i - 1);
            //得到所有可能的右子树
            List<TreeNode> rightTrees = getAns(i + 1, end);
            //左子树右子树两两组合
            for (TreeNode leftTree : leftTrees) {
                for (TreeNode rightTree : rightTrees) {
                    TreeNode root = new TreeNode(i);
                    root.left = leftTree;
                    root.right = rightTree;
                    //加入到最终结果中
                    ans.add(root);
                }
            }
        }
        return ans;
    }

动态规划

斐波那契数列

爬楼梯，抢劫，环形抢劫（将首尾节点各自切掉之后得到2种情况后比大小）

4. 信件错排

题目描述：有 N 个 信 和 信封，它们被打乱，求错误装信方式的数量。

定义一个数组 dp 存储错误方式数量，dp[i] 表示前 i 个信和信封的错误方式数量。假设第 i 个信装到第 j 个信封里面，而第 j 个信装到第 k 个信封里面。根据 i 和 k 是否相等，有两种情况：1：i==k,i!=k;

dp[i] = (i-1)dp[i-2] + (i-1)dp[i-1]

母牛生产

dp[ i ]=dp[i-1]+dp[i-3]

矩阵路径

1. 矩阵的最小路径和2. 矩阵的总路径数

题目描述：求从矩阵的左上角到右下角的最小路径和，每次只能向右和向下移动。

2道题不用额外空间的解法没看

数组区间

1. 数组区间和

1
2
3
4
5
Given nums = [-2, 0, 3, -5, 2, -1]
sumRange(0, 2) -> 1
sumRange(2, 5) -> -1
sumRange(0, 5) -> -3

求区间 i ~ j 的和，可以转换为 sum[j + 1] - sum[i]，其中 sum[i] 为 0 ~ i - 1 的和。

2. 数组中等差递增子区间的个数

1
2
3
4
5
6
7
8
9
10
A = [0, 1, 2, 3, 4]
return: 6, for 3 arithmetic slices in A:
[0, 1, 2],
[1, 2, 3],
[0, 1, 2, 3],
[0, 1, 2, 3, 4],
[ 1, 2, 3, 4],
[2, 3, 4]

dp[i] 表示以 A[i] 为结尾的等差递增子区间的个数。

当 A[i] - A[i-1] == A[i-1] - A[i-2]，那么 [A[i-2], A[i-1], A[i]] 构成一个等差递增子区间。而且在以 A[i-1] 为结尾的递增子区间的后面再加上一个 A[i]，一样可以构成新的递增子区间。

1
2
3
4
5
6
7
8
9
dp[2] = 1
    [0, 1, 2]
dp[3] = dp[2] + 1 = 2
    [0, 1, 2, 3], // [0, 1, 2] 之后加一个 3
    [1, 2, 3]     // 新的递增子区间
dp[4] = dp[3] + 1 = 3
    [0, 1, 2, 3, 4], // [0, 1, 2, 3] 之后加一个 4
    [1, 2, 3, 4],    // [1, 2, 3] 之后加一个 4
    [2, 3, 4]        // 新的递增子区间

综上，在 A[i] - A[i-1] == A[i-1] - A[i-2] 时，dp[i] = dp[i-1] + 1。

因为递增子区间不一定以最后一个元素为结尾，可以是任意一个元素结尾，因此需要返回 dp 数组累加的结果。

cht注：抄的，当时不会做。。。。。

分割整数

1. 分割整数的最大乘积

给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 返回你可以获得的最大乘积。

题目描述：For example, given n = 2, return 1 (2 = 1 + 1); given n = 10, return 36 (10 = 3 + 3 + 4).

思路：2层for循环，注意如果不拆分也有可能比拆分的乘积大。

2. 按平方数来分割整数

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, ...）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。

题目描述：For example, given n = 12, return 3 because 12 = 4 + 4 + 4; given n = 13, return 2 because 13 = 4 + 9.

思路：我觉得我的解法更不错。

3. 分割整数构成字母字符串

一条包含字母 A-Z 的消息通过以下方式进行了编码：

‘A’ -> 1
‘B’ -> 2
…
‘Z’ -> 26
给定一个只包含数字的非空字符串，请计算解码方法的总数。

示例 1:

输入: “12”
输出: 2
解释: 它可以解码为 “AB”（1 2）或者 “L”（12）。
示例 2:

输入: “226”
输出: 3
解释: 它可以解码为 “BZ” (2 26), “VF” (22 6), 或者 “BBF” (2 2 6) 。

抄的，当时不会做。

思路：dp[i]+=dp[i-1] ；如果当前数字与前一位组合的数字处于10-26时，再加dp[i-2]

最长递增子序列

1. 最长递增子序列

给定一个无序的整数数组，找到其中最长上升子序列的长度。

思路：两层for循环，第二层循环里面遍历找到所有比当前数小的数，做memo[i]的重新赋值（和最大值比较再赋值）

2. 一组整数对能够构成的最长链

给出 n 个数对。 在每一个数对中，第一个数字总是比第二个数字小。

现在，我们定义一种跟随关系，当且仅当 b < c 时，数对(c, d) 才可以跟在 (a, b) 后面。我们用这种形式来构造一个数对链。

给定一个对数集合，找出能够形成的最长数对链的长度。你不需要用到所有的数对，你可以以任何顺序选择其中的一些数对来构造。

示例 :

输入: [[1,2], [2,3], [3,4]]
输出: 2
解释: 最长的数对链是 [1,2] -> [3,4]

思路：先排序，然后和上面一题一样。

3. 最长摆动子序列

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为摆动序列。第一个差（如果存在的话）可能是正数或负数。少于两个元素的序列也是摆动序列。

例如， [1,7,4,9,2,5] 是一个摆动序列，因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

给定一个整数序列，返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些（也可以不删除）元素来获得子序列，剩下的元素保持其原始顺序。

思路：定义一个up和一个down，GitHub解法o(n);【牛逼的】

最长公共子序列

思路：对于两个子序列 S1 和 S2，找出它们最长的公共子序列。

定义一个二维数组 dp 用来存储最长公共子序列的长度，其中 dp[i][j] 表示 S1 的前 i 个字符与 S2 的前 j 个字符最长公共子序列的长度。考虑 S1i 与 S2j 值是否相等，分为两种情况：

  • 当 S1i==S2j 时，那么就能在 S1 的前 i-1 个字符与 S2 的前 j-1 个字符最长公共子序列的基础上再加上 S1i 这个值，最长公共子序列长度加 1，即 dp[i][j] = dp[i-1][j-1] + 1。
  • 当 S1i != S2j 时，此时最长公共子序列为 S1 的前 i-1 个字符和 S2 的前 j 个字符最长公共子序列，或者 S1 的前 i 个字符和 S2 的前 j-1 个字符最长公共子序列，取它们的最大者，即 dp[i][j] = max{ dp[i-1][j], dp[i][j-1] }。

综上，最长公共子序列的状态转移方程为：

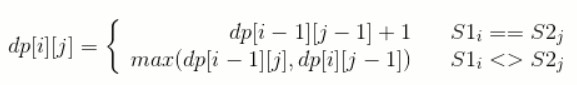
image

与最长递增子序列不同的是，而最长递增子序列中 dp[N] 不是最终解，因为以 Sn 为结尾的最长递增子序列不一定是整个序列最长递增子序列，需要遍历一遍 dp 数组找到最大者。

0-1 背包

1
dp[i][j] 表示前 i 件物品体积不超过 j 的情况下能达到的最大价值。

image

1. 划分数组为和相等的两部分

可以看成一个背包大小为 sum/2 的 0-1 背包问题。只不过这里不要求求出最大的value，而是看能不能等于一个指定的value，因此函数返回boolean

部分函数体：

1
2
3
4
5
6
7
8
for (int i = 1; i < size; i++) {
           for (int j = 0; j < target + 1; j++) {
               dp[i][j] = dp[i - 1][j];
               if (j >= nums[i]) {
                   dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i]];
               }
           }
       }

2. 改变一组数的正负号使得它们的和为一给定数

1
2
3
4
5
6
7
8
9
10
11
Input: nums is [1, 1, 1, 1, 1], S is 3.
Output: 5
Explanation:
-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3
There are 5 ways to assign symbols to make the sum of nums be target 3.

该问题可以转换为 Subset Sum 问题，从而使用 0-1 背包的方法来求解。

可以将这组数看成两部分，P 和 N，其中 P 使用正号，N 使用负号，有以下推导：

1
2
3
                  sum(P) - sum(N) = target
sum(P) + sum(N) + sum(P) - sum(N) = target + sum(P) + sum(N)
                       2 * sum(P) = target + sum(nums)

因此只要找到一个子集，令它们都取正号，并且和等于 (target + sum(nums))/2，就证明存在解。

思路：1dp2dfs

3. 01 字符构成最多的字符串

在计算机界中，我们总是追求用有限的资源获取最大的收益。

现在，假设你分别支配着 m 个 0 和 n 个 1。另外，还有一个仅包含 0 和 1 字符串的数组。

你的任务是使用给定的 m 个 0 和 n 个 1 ，找到能拼出存在于数组中的字符串的最大数量。每个 0 和 1 至多被使用一次。

注意:

给定 0 和 1 的数量都不会超过 100。
给定字符串数组的长度不会超过 600。

1
2
3
4
5
6
示例 1:
输入: Array = {"10", "0001", "111001", "1", "0"}, m = 5, n = 3
输出: 4
解释: 总共 4 个字符串可以通过 5 个 0 和 3 个 1 拼出，即 "10","0001","1","0" 。

这是一个多维费用的 0-1 背包问题，有两个背包大小，0 的数量和 1 的数量

不看了，自己玩吧

4. 找零钱的最少硬币数

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

示例 1:

输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public int coinChange(int[] coins, int amount) {//和背包没啥关系吧 直接用dp
        memo = new int[amount+1];
        for (int i = 0; i < amount + 1; i++) {
            memo[i] = Integer.MAX_VALUE - 1;
        }
        memo[0] = 0;
        for (int i = 1; i < amount + 1; i++) {
            for (int coin:coins){
                if(coin<=i)
                    memo[i] = Math.min(memo[i],1 + memo[i-coin]);
            }
        }
        return memo[amount] > Integer.MAX_VALUE - 2 ? -1 : memo[amount];
    }

和背包没啥关系吧 直接用dp,徒手想。

5. 找零钱的硬币数组合

1
2
3
4
5
6
7
8
9
10
11
输入: amount = 5, coins = [1, 2, 5]
输出: 4
解释: 有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/coin-change-2
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
1
2
3
4
5
6
7
8
9
10
public int change(int amount, int[] coins) {
        int[] memo = new int[amount+1];
        memo[0] = 1;
        for (int coin:coins){
            for (int i = coin; i < amount + 1; i++) {//注意先循环coins 再循环i->amount+1
                    memo[i] += memo[i-coin];
            }
        }
        return memo[amount];
    }

也不必刻意想成他所说的背包基础上的问题

6. 字符串按单词列表分割

todo

7. 组合总和

给定一个由正整数组成且不存在重复数字的数组，找出和为给定目标正整数的组合的个数。

todo

股票交易

所有状态

1
2
3
4
5
6
7
8
9
dp[i][k][0 or 1]
0 <= i <= n-1, 1 <= k <= K
n 为天数，大 K 为最多交易数
此问题共 n × K × 2 种状态，全部穷举就能搞定。
for 0 <= i < n:
    for 1 <= k <= K:
        for s in {0, 1}:
            dp[i][k][s] = max(buy, sell, rest)

状态转移框架

1
2
3
4
5
6
7
8
9
10
11
12
13
14
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
              max(   选择 rest  ,           选择 sell      )
解释：今天我没有持有股票，有两种可能：
要么是我昨天就没有持有，然后今天选择 rest，所以我今天还是没有持有；
要么是我昨天持有股票，但是今天我 sell 了，所以我今天没有持有股票了。
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
              max(   选择 rest  ,           选择 buy         )
解释：今天我持有着股票，有两种可能：
要么我昨天就持有着股票，然后今天选择 rest，所以我今天还持有着股票；
要么我昨天本没有持有，但今天我选择 buy，所以今天我就持有股票了。

初始值

1
2
3
4
5
6
7
8
dp[-1][k][0] = 0
解释：因为 i 是从 0 开始的，所以 i = -1 意味着还没有开始，这时候的利润当然是 0 。
dp[-1][k][1] = -infinity
解释：还没开始的时候，是不可能持有股票的，用负无穷表示这种不可能。
dp[i][0][0] = 0
解释：因为 k 是从 1 开始的，所以 k = 0 意味着根本不允许交易，这时候利润当然是 0 。
dp[i][0][1] = -infinity
解释：不允许交易的情况下，是不可能持有股票的，用负无穷表示这种不可能。

总结

1
2
3
4
5
6
7
8
9
10
base case：
dp[-1][k][0] = dp[i][0][0] = 0
dp[-1][k][1] = dp[i][0][1] = -infinity
状态转移方程：
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
我们想求的最终答案是 dp[n - 1][K][0]，即最后一天，最多允许 K 次交易，最多获得多少利润。

字符串编辑

1. 删除两个字符串的字符使它们相等

给定两个单词 word1 和 word2，找到使得 word1 和 word2 相同所需的最小步数，每步可以删除任意一个字符串中的一个字符。

1
2
3
Input: "sea", "eat"
Output: 2
Explanation: You need one step to make "sea" to "ea" and another step to make "eat" to "ea".

思路：可以转换为求两个字符串的最长公共子序列问题。

斐波拉切数列

爬楼梯，抢劫，环形抢劫（将首尾节点各自切掉之后得到2种情况后比大小）

数组区间

数组中等差递增子区间的个数：在 A[i] - A[i-1] == A[i-1] - A[i-2] 时，dp[i] = dp[i-1] + 1。

分治整数

分割整数的最大乘积：2层for循环，注意如果不拆分也有可能比拆分的乘积大；思路：dp[i]+=dp[i-1] ；分割整数构成字母字符串：如果当前数字与前一位组合的数字处于10-26时，再加dp[i-2]；最长递增子序列思路：两层for循环，第二层循环里面遍历找到所有比当前数小的数，做memo[i]的重新赋值（和最大值比较再赋值）； 一组整数对能够构成的最长链：先排序，然后和上面一题一样。最长摆动子序列：思路：定义一个up和一个down，GitHub解法o(n);【牛逼的】；最长公共子序列：考虑2种情况；

0-1 背包

dp [i] [j] = max（dp [i-1] [j]，dp [i-1] [j-w] + v）【空间优化：dp [ j ] = max(dp [j] , dp [i-1] + v)】

划分数组为和相等的两部分：可以看成一个背包大小为 sum/2 的 0-1 背包问题。改变一组数的正负号使得它们的和为一给定数：可以转换为 Subset Sum 问题；找零钱的最少硬币数； 找零钱的硬币数组合；

股票交易

搜索

BFS

1. 计算在网格中从原点到特定点的最短路径长度

1
2
3
4
[[1,1,0,1],
 [1,0,1,0],
 [1,1,1,1],
 [1,0,1,1]]

题目描述：1 表示可以经过某个位置，求解从 (0, 0) 位置到 (tr, tc) 位置的最短路径长度。

思路：BFS 就像层次遍历似的

2. 组成整数的最小平方数数量

1
For example, given n = 12, return 3 because 12 = 4 + 4 + 4; given n = 13, return 2 because 13 = 4 + 9.

可以将每个整数看成图中的一个节点，如果两个整数之差为一个平方数，那么这两个整数所在的节点就有一条边。

要求解最小的平方数数量，就是求解从节点 n 到节点 0 的最短路径。

思路：注意队列加标记

3. 最短单词路径（单词接龙）

给定两个单词（beginWord 和 endWord）和一个字典，找到从 beginWord 到 endWord 的最短转换序列的长度。转换需遵循如下规则：

每次转换只能改变一个字母。
转换过程中的中间单词必须是字典中的单词。

说明:

如果不存在这样的转换序列，返回 0。
所有单词具有相同的长度。
所有单词只由小写字母组成。
字典中不存在重复的单词。
你可以假设 beginWord 和 endWord 是非空的，且二者不相同。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Input:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]
Output: 5
Explanation: As one shortest transformation is "hit" -> "hot" -> "dot" -> "dog" -> "cog",
return its length 5.
Input:
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]
Output: 0
Explanation: The endWord "cog" is not in wordList, therefore no possible transformation.

思路：步骤和准备工作比较多，但终究还是BFS，注意图的节点存的是字符串在wordlist里的索引，不是字符串本身。

DFS

1. 查找最大的连通面积

给定一个包含了一些 0 和 1的非空二维数组 grid , 一个 岛屿 是由四个方向 (水平或垂直) 的 1 (代表土地) 构成的组合。你可以假设二维矩阵的四个边缘都被水包围着。

找到给定的二维数组中最大的岛屿面积。(如果没有岛屿，则返回面积为0。)

示例 1:

1
2
3
4
5
6
7
8
[[0,0,1,0,0,0,0,1,0,0,0,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,1,1,0,1,0,0,0,0,0,0,0,0],
 [0,1,0,0,1,1,0,0,1,0,1,0,0],
 [0,1,0,0,1,1,0,0,1,1,1,0,0],
 [0,0,0,0,0,0,0,0,0,0,1,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,0,0,0,0,0,0,1,1,0,0,0,0]]

对于上面这个给定矩阵应返回 6。注意答案不应该是11，因为岛屿只能包含水平或垂直的四个方向的‘1’。

思路：递归，标记

2. 矩阵中的连通分量数目

1
2
3
4
5
6
7
Input:
11000
11000
00100
00011
Output: 3

求岛屿的数量

思路：递归，标记，与上题不同的是DFS 不返回值，作用仅仅是把可以连通的标记置为‘0’

3. 好友关系的连通分量数目

1
2
3
4
5
6
7
8
9
Input:
[[1,1,0],
 [1,1,0],
 [0,0,1]]
Output: 2
Explanation:The 0th and 1st students are direct friends, so they are in a friend circle.
The 2nd student himself is in a friend circle. So return 2.

题目描述：好友关系可以看成是一个无向图，例如第 0 个人与第 1 个人是好友，那么 M[0][1] 和 M[1][0] 的值都为 1。

思路：递归，标记；与上题不同的是：上题是个无向图，这里是有向图，主函数只要一层循环，还需要一个一维数组。

4. 填充封闭区域

给定一个二维的矩阵，包含 ‘X’ 和 ‘O’（字母 O）。

找到所有被 ‘X’ 围绕的区域，并将这些区域里所有的 ‘O’ 用 ‘X’ 填充。

示例:

X X X X
X O O X
X X O X
X O X X
运行你的函数后，矩阵变为：

X X X X
X X X X
X X X X
X O X X
解释:

被围绕的区间不会存在于边界上，换句话说，任何边界上的 ‘O’ 都不会被填充为 ‘X’。 任何不在边界上，或不与边界上的 ‘O’ 相连的 ‘O’ 最终都会被填充为 ‘X’。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

思路：先填充最外侧，剩下的就是里侧了。（把外侧的O换成T,最后遍历时把所有O换成X,所有T换成O）

5. 能到达的太平洋和大西洋的区域

给定一个 m x n 的非负整数矩阵来表示一片大陆上各个单元格的高度。“太平洋”处于大陆的左边界和上边界，而“大西洋”处于大陆的右边界和下边界。

规定水流只能按照上、下、左、右四个方向流动，且只能从高到低或者在同等高度上流动。

请找出那些水流既可以流动到“太平洋”，又能流动到“大西洋”的陆地单元的坐标。

1
2
3
4
5
6
7
8
9
10
11
12
Given the following 5x5 matrix:
  Pacific ~   ~   ~   ~   ~
       ~  1   2   2   3  (5) *
       ~  3   2   3  (4) (4) *
       ~  2   4  (5)  3   1  *
       ~ (6) (7)  1   4   5  *
       ~ (5)  1   1   2   4  *
          *   *   *   *   * Atlantic
Return:
[[0, 4], [1, 3], [1, 4], [2, 2], [3, 0], [3, 1], [4, 0]] (positions with parentheses in above matrix).

思路：先填充最外侧for (int i = 0; i < m; i++) {...} for (int i = 0; i < n; i++) {...}

回溯

1. 数字键盘组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

img

1
2
Input:Digit string "23"
Output: ["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].

思路：递归的函数：先写出口条件，再写循环，循环里：先写追加元素，然后递归调用，最后删除（回退）；我的解法由于函数最后一个参数传的是s+new str 这种形式，所以不用回退。【also in mk】。我的解法需要一个全局的list在递归出口处add（s）,s来保存当前已有元素。

2. IP 地址划分

给定一个只包含数字的字符串，复原它并返回所有可能的 IP 地址格式。

示例:

输入: “25525511135”
输出: [“255.255.11.135”, “255.255.111.35”]

思路：【also in mk】需要一个全局list：ans 在递归出口处add一个叫cur的List，cur来保存当前已有元素

// 该题可以看成如何分割串（分割完之后再split）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// cur : 当前答案，以 String List的形式，最后再join成String形式 例如 [[255],[255],[111],[35]] -> 255.255.111.35
// pos, 当前扫描到的s的位置， ans最终答案
private void backtracking(String s, int pos, List<String> cur,  List<String> ans) {
    if (cur.size() >= 4) {
        if (pos == s.length()) ans.add(String.join(".", cur));
        return;
    }
    // 分割得到ip地址的一段后，下一段只能在长度1-3范围内选择
    for (int i = 1; i <= 3; i++) {
        if (pos+i > s.length()) break;
        String segment = s.substring(pos, pos+i);
        // 剪枝条件：不能以0开头，不能大于255
        if (segment.startsWith("0") && segment.length() > 1 || (i == 3 && Integer.parseInt(segment) > 255)) continue;
        cur.add(segment);
        // 注意此处传的参数
        backtracking(s, pos+i, cur, ans);
        cur.remove(cur.size()-1);
    }
}
public List<String> restoreIpAddresses(String s) {
    List<String> ans = new ArrayList<>();
    backtracking(s, 0, new ArrayList<>(), ans);
    return ans;
}

3. 在矩阵中寻找字符串

【also in mk】

1
2
3
4
5
6
7
8
9
10
For example,
Given board =
[
  ['A','B','C','E'],
  ['S','F','C','S'],
  ['A','D','E','E']
]
word = "ABCCED", -> returns true,
word = "SEE", -> returns true,
word = "ABCB", -> returns false.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
private int r;
    private int c;
    private int[][] direction = {{1,0},{-1,0},{0,1},{0,-1}};
    private boolean[][] visited ;
    public boolean exist(char[][] board, String word) {//用的是 慕课算法提供的思路
        if (word == null || word.length() == 0) {
            return true;
        }
        if (board == null || board.length == 0 || board[0].length == 0) {
            return false;
        }
        int r = board.length;
        int c = board[0].length;
        this.r = r;
        this.c = c;
        visited = new boolean[r][c];
        for (int i = 0; i < r; i++) {
            for (int j = 0; j < c; j++) {
                if(foo(board,word,0,i,j))
                    return true;
            }
        }
        return false;
    }
    private boolean foo(char[][] board, String word, int index,int i,int j) {
        if(index==word.length()-1){
            return board[i][j] == word.charAt(index);
        }
        if(board[i][j]==word.charAt(index)){
            visited[i][j] = true;
            for (int[] arr:direction){
                int newI = i+arr[0];
                int newJ = j+arr[1];
                if((newI>=0&&newI<r&&newJ>=0&&newJ<c)&&!visited[newI][newJ]&&foo(board,word,index+1,newI,newJ))
                    return true;
            }
            visited[i][j] = false;
        }
        return false;
    }

需要一个访问标记数组

4. 输出二叉树中所有从根到叶子的路径

1
2
3
4
5
6
  1
 /  \
2    3
 \
  5
["1->2->5", "1->3"]

思路：我的解法没有回退的操作，是因为：我在传字符串时是 以 s + newstr 的形式。而GitHub解法需要一个全局的List：paths,在isLead() 为true 时 add 一个叫values的list。

5. 排列

给定一个没有重复数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]

思路：可以看到需要一个全局的list 在递归出口时 add(curList),一个当前元素的list：curList。一个访问标记数组

6. 含有相同元素求排列

1
2
1,1,2] have the following unique permutations:
[[1,1,2], [1,2,1], [2,1,1]]

数组元素可能含有相同的元素，进行排列时就有可能出现重复的排列，要求重复的排列只返回一个。

在实现上，和 Permutations 不同的是要先排序，然后在添加一个元素时，判断这个元素是否等于前一个元素，如果等于，并且前一个元素还未访问，那么就跳过这个元素。

7. 组合

给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。

1
2
3
4
5
6
7
8
9
If n = 4 and k = 2, a solution is:
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]
1
for (int i = start; i <= n ); i++) {
1
2
//还有k-item.size()个空位，所以[i...n]中至少要有k-item.size()个元素
for (int i = start; i <= n + 1 - (k - item.size()); i++) {//剪枝

8. 组合求和

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

1
2
3
given candidate set [2, 3, 6, 7] and target 7,
A solution set is:
[[7],[2, 2, 3]]

9. 含有相同元素的组合求和

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

说明：

所有数字（包括目标数）都是正整数。
解集不能包含重复的组合。 

1
2
3
4
5
6
7
8
For example, given candidate set [10, 1, 2, 7, 6, 1, 5] and target 8,
A solution set is:
[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]

注意：和6一样：先排序，在添加一个元素时，判断这个元素是否等于前一个元素，如果等于，并且前一个元素还未访问，那么就跳过这个元素。

10. 1-9 数字的组合求和

找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

说明：

所有数字都是正整数。
解集不能包含重复的组合。

11. 子集

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

also in mk

总结：对于解集不能包含重复的组合，像11,10,9（还有8，7）；for循环都得从start开始

12. 含有相同元素求子集

给定一个可能包含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

相比11，先排序，在添加一个元素时，判断这个元素是否等于前一个元素，如果等于，并且前一个元素还未访问，那么就跳过这个元素。

13. 分割字符串使得每个部分都是回文数

给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。

返回 s 所有可能的分割方案。

1
2
3
4
5
6
7
For example, given s = "aab",
Return
[
  ["aa","b"],
  ["a","a","b"]
]

思路：也是for(i=start…..)

14. 数独

todo

15. N 皇后

image

返回所有解法

思路：定义一个列访问位数组，一个正对角线访问位数组（i+j），一个斜对角线访问位数组(i-j)

分享到： 收藏夹 复制网址 邮件 微信 QQ空间 腾讯微博 豆瓣 一键分享 更多